МЕТОДЫ АНАЛИЗА И ОПТИМИЗАЦИИ ЭФФЕКТИВНОСТИ СЛОЖНЫХ СИСТЕМ И ПРОЦЕССОВ

Программно-целевой подход к управленню эффективностью сложных систем и процессов предполагает увязку показателей эф­фективности, целей и средств с помощью математических моделей. Моделирование эффективности включает: системный анализ объ­екта, определение целей и задач исследования; выбор показателей и критериев эффективности; разработку математической модели принятия решения; разработку алгоритма поиска оптимального решения; проверку модели и оценку ее качества; моделирование; анализ результатов и подготовку данных для принятия решения.

При построении математических моделей эффективности руко­водствуются следующими требованиями: модель должна описывать объект с достаточной полнотой и обладать свойством эволюцион — ности; степень абстрактности модели не должна вызывать сомне­ний относительно ее практической полезности; модель должна пре­дусматривать возможность получения хотя бы приближенного ре­шения задачи к требуемому моменту времени; должно быть пре­дусмотрено использование ЭВМ.

Общие принципы построения математических моделей функцио­нирования воздушного транспорта представляют собой общие принципы теории систем [11]. Отличительной чертой любой системы является наличие у нее входа и выхода. Для входа существуют та­кие названия, как причина, стимул, воздействие, возмущение, ре-

суре, план, команда и т. п., а для выхода — следствие, эффект, от­вет, реакция, факт и т. д. Опре­деленное изменение входной ве­личины системы влечет за собой некоторое изменение и выходной величины.

Зависимость входной величи­ны от выходной определяется за­коном поведения системы. В иде­альном случае этот закон может быть выражен в виде математического ‘уравнения, допускающего общее аналитическое решение. В такое уравнение входит некото­рое число постоянных величин или параметров, характеризующих определенные свойства систем. Систему, определяемую в такой общей форме, можно представить графически (рис. 1.4) или ана­литически в виде бинарного отношения

(U, X)]Rx Y — ((С, X), Y) ЕЕ Ru ЕЕ (U X X)Y, (1.15)

где U=V(t)—вектор, определяющий множество входов системы; Х=Х(t) — вектор, определяющий, множество параметров состояния системы; V=V(t) — вектор, определяющий множество‘переменных внешней среды, влияющих на со­стояние системы (через U); Y=Y(t) — вектор, определяющий множество выхо­дов системы; Ri — бинарное отношение, в соответствии с которым система пре — образует входы в выходы.

Представленная на рис. 1.4 система может быть также выраже­на в виде функционального отношения

Y = <3?! (U, X, V), (1.16)

где Ф(—функциональный оператор, в соответствии с которым система преобра­зует входы в выходы.

Математические отношения (1.15) и (1.16), в соответствии с которыми система преобразует входы в выходы, называются мате­матическими моделями ее функционирования. Содержание векто­ров U, X, V и Y зависит от характера рассматриваемой системы, целей и задач ее функционирования и задач проводимых исследо­ваний. В общем случае вход системы может трактоваться как при­чина, а выход как следствие. Для технических систем характерно их описание в понятиях «вход — выход — состояние». Причем вы­ход часто отождествляется с состоянием. Для больших систем (организационных и человеко-машинных) вход и выход тракту­ются в понятиях целей и результатов функционирования; входами обычно бывают ресурсы, определяемые в соответствии с целями, а выходами — результаты решения задач и достижения целей.

С точки зрения системного подхода все многообразие задач ис­следования эффективности может быть сведено к четырем типовым задачам.

Задача 1. Известны входные величины, закон поведения и свойства системы, а также входы от внешней среды. Требуется оп-

ределить выходные величины или законы их изменения. Такого типа «прямые» и другие подобные задачи наиболее просты и часто встречаются в инженерной практике оценки и прогнозирования производственной деятельности предприятий, возможностей пред­приятий, оценки надежности, и эффективности самолетов и других образцов авиационной техники. Задачи данного типа — это задачи оценки эффекта при заданных затратах.

Задача 2. Заданы закон поведения системы, ее свойства, вы­ход и параметры входа от внешней среды. Необходимо определить вход, обеспечивающий получение заданного выхода. Эта задача («обратная» первого рода) представляет собой одну из задач опре­деления необходимых затрат для достижения заданного эффекта. К этому типу задач относятся также задачи диагностирования.

Задача 3. Заданы вход, выход и общий вид закона поведения системы, а также параметры внешней среды. Требуется определить параметры состояния системы и ее свойства. Это «обратная» зада­ча второго рода. Задачи данного типа получили в инженерной практике название задач синтеза. Они решаются при проектирова­нии технических систем, разработке программ и планов развития предприятий и т. д.

Задача 4. Известны лишь вход и выход системы. Требуется определить закон поведения и значения отдельных параметров и свойств системы. Такая задача индукции (или «черного ящика») представляет собой наиболее сложную форму задачи синтеза. За­дачи этого типа наиболее часто встречаются в практике перспек­тивного планирования и прогнозирования и решаются методами регрессионного, корреляционного анализа и другими методами ста­тистического анализа и проверки статистических гипотез (см. п. 2.4 гл. II)’ Формализованное описание перечисленных задач зависит от уровня их структуризации.

Структура любой задачи определяется пятью основными эле­ментами, к которым относятся: цель или ряд целей, достижение которых будет означать решение поставленной задачи; альтерна­тивные средства, т. е. курсы действий, с помощью которых может быть достигнута цель; затраты ресурсов, требуемых для каждого курса действий; модель или система моделей, з которых с помощью некоторого формального языка (математики, формальной логики, обычного словесного, графического или машинного описания и т. п.) отображаются связи между целями, альтернативами и затра­тами; критерий, с помощью которого сопоставляются цели и затра­ты для их достижения. Уровень структуризации задачи определя­ется тем, насколько хорошо выделены и формализованы указанные выше пять логических элементов, а от этого, в свою очередь, зави­сят вид моделей и метод экономико-математического моделирова­ния. С точки зрения возможностей применения существующих ме­тодов математического моделирования встречающиеся на практике проблемы можно разделить на четыре группы задач: стандартные; хорошо структуризованные; слабоструктуризованные; неструкту — ризованные.

Стандартные задачи моделирования отличаются частой повторяемостью, полной ясностью и однозначностью не только це­лей, альтернатив и задач, но и самих решений. Эти задачи реша­ются на основе стандартных моделей, основанных на заранее вы­работанных процедурах и правилах и помещенных в официальных; методиках vi стандартах (ОСТ и ГОСТ). К стандартным задачам, например, относятся: расчет потребности в оборудовании, рабочей силе и материалах исходя из заданной производственной програм­мы предприятия; расчет технико-экономических показателей про­изводственно-финансового плана предприятия при заданных исход­ных данных, которые считаются точными и достоверными, и многие подобные планово-производственные задачи. К стандартным моде­лям, например, относится балансовая матричная модель техпром — финплана предприятия, включающая заданные нормативы — коэф­фициенты прямых и полных затрат. Стандартные задачи и модели встречаются часто в практической деятельности экономистов — на предприятиях и в учреждениях. Выполняемые при этом расчеты, как правило, одновариантные. Результаты расчетов служат исход — n ной информацией для принятия решений.

Хорошо структуризованные задачи моделирования по своему существу многовариантны, но все их элементы и связи на­столько хорошо изучены, что могут быть выражены количественно с помощью функциональных зависимостей. К этой группе задач от­носятся: выбор оптимального варианта развития и реконструкции предприятия; вариантов наилучшей загрузки производственных мощностей; поиск оптимальных технологических режимов; выбор оптимальных планов замены оборудования; технического обслужи­вания и ремонта техники; распределения самолетов по воздушным линиям и многие другие. Задачи данной группы решаются с ис­пользованием оптимизационных математических моделей (метода­ми математического программирования).

Слабоструктуризованные задачи моделирования, как правило, связаны с перспективным развитием системы и ее элемен­тов (подсистем), а также с решением задач управления в условиях неопределенности исходной информации. Задачи этой группы ре­шаются с использованием имитационных математических моделей, в которых используются стандартные и оптимизационные модели для решения отдельных частных задач, но окончательное решение принимается руководителем с использованием неформальных ме­тодов системного анализа.

Неструктуризованные задачи отличаются невозможностью ма­тематической формализации системы целей и возможных стратегий их достижения. Для задач этой группы фактор неопределенности приобретает решающее значение. К этой группе задач относятся, например, задачи формирования долгосрочного плана развития воздушного транспорта, задачи формирования комплексных про­грамм развития технической, технологической, экономической, со­циальной и организационной систем, а также многие другие зада­чи, решаемые на уровне отрасли. При решении задач этой группы

применяют эвристические модели принятия решений. Другие виды математических моделей (стандартные, оптимизационные и имита­ционные) испрльзуются при этом в качестве инструмента обработ­ки исходной информации для принятия решений.

В зависимости от уровня структуризации задач моделирования эффективности на практике используются стандартные, оптимиза­ционные, имитационные или эвристические модели. Все они полу­чаются на основе следующей обобщенной модели управления эф­фективностью системы [38]:

w — ф%0,o]).^extr;

х (t) — Fi (х°; t; “р0ф #[<„,<])! y(t) ^F2(y°; t xUo t]- и[(оі(,); x<>, Xі EE Q [x]; и EE Q [a]; y°,yi^Q[y]-, t ЄЕ [^i],

где W—критерий эффективности прошводства; fij —отрезок вектор-функ­ции, характеризующий уровень развития (состояния) и производства на интерва­ле р0, ^]; И[(01 <,] —отрезок вектор-функции, характеризующий распределение производственных ресурсов да том же интервале; У^^ tl] —отрезок вектор-функ­ции, характеризующий конечный результат производства на интервале • [Д М; x{t) ■—вектор состояния производства в момент t x°—x(t0)—начальное сос­тояние производства (состояние в. начале планового периода); xl=x(tl)—-сос­тояние производства в конце — планового — периода; y(t)—вектор конечного ре­зультата производства в момент t y°—y(t0) и yl = y{ti)—значения y(t) в мо­мент U я ti соответственно; Q[u], Q[x Q[t/] — ограничения; Ф(-), Fi(-) — F2( • ) — операторы.

На основе этой модели может быть построена оптимальная си­стема управления эффективностью воздушного транспорта, кото­рая обеспечит получение оптимального плана:

П*= (и[<о, М; ^оф])’ . (LI8>

где ut0tt, — отрезок вектор-функции оптимального распределения ресурсов на интервале [*о, к\ xt0,/,] —отрезок вектор-фу-нкции оптимального развития производства на интервале [f0, У; y[to, ti] — отрезок вектор-функции оптималь­ного — конечного результата производства на интервале Щ, ti.

Следовательно, задача управления эффективностью производст­ва воздушного транспорта сводится к построению такого плана использования ресурсов для получения конечного резуль­тата yt0,tl] и развития производства, который обеспечи­

вает оптимальное значение W* критерия эффективности производ­ства W.

Функционал Ф и операторы Fi и F2 могут быть аналитическими функциями или же представлять собой некоторые другие матема­тические отношения. В зависимости от степени информированности об операторах Рг и F2 различают три постановки задачи управле­ния эффективностью производства воздушного транспорта: детер­минированную, стохастическую (вероятностную) и игровую (ми­нимаксную). Поскольку производство воздушного транспорта

представляет собой стохастическую систему, задача управления его’ эффективностью должна решаться в стохастической постановке. При этом в зависимости от вида Ф, F и F2 модель (1.17) может быть стандартной, оптимизационной, имитационной или эвристи­ческой.

Если операторы /д, Р2 и Ф заданы аналитическими функциями с известными параметрами и альтернативы отсутствуют, то модель (2.17) будет стандартной. При заданных аналитических функциях Fu F2, Ф и наличии альтернатив модель становится оптимизацион­ной. Если операторы /д и F2 имеют аналитическое выражение, а Ф не имеет, то модель (4.1) становится имитационной. Если хотя бы один из операторов 7д или F2 не имеет аналитического выраже­ния, то модель (2.17) будет эвристической.

Построение стандартных математических моделей не вызывает затруднений. Разработка других видов моделей встречает на пути много препятствий, из которых важнейшими являются слабая структуризация решаемых задач и неопределенность исходной ин­формации.

Полнота, точность, достоверность и своевременность получения необходимой информации является решающим условием успешно­го применения методов математического моделирования в системе управления эффективностью производства воздушного транспорта.

Несколько замечаний по поводу информационного обеспечения задач, решаемых при исследовании эффективности воздушного транспорта. Общее представление о составе необходимой исходной для исследования эффективности информации можно получить на основе анализа приведенных выше обобщенных математических моделей, из которых следует, что для анализа и оценки эффектив­ности необходимо иметь прежде всего информацию о целях функ­ционирования и развития системы воздушного транспорта,, ресур­сах, состоянии системы и поведении внешней среды.

При разработке математических моделей необходимо тщатель­но изучать и максимально использовать сложившуюся в граждан­ской авиации систему измерителей, показателей и критериев, явля­ющихся носителями агрегированной информации о системах и про­цессах воздушного транспорта. Математические модели эффектив­ности, разработанные без учета функционирующей в отрасли сис­темы информации, встретят огромные трудности на пути внедре­ния, которые могут оказаться непреодолимыми.

Важное влияние на возможности построения и использования математических моделей оказывает неопределенность информации, что связано с необходимостью использования результатов прогно­зирования спроса на пассажирские и грузовые перевозки, исполь­зования в перспективе ныне неизвестных результатов научно-тех­нического прогресса, а также развития. внешней среды. На первый взгляд, наилучшим способом снятия неопределенности внешней ин­формации является расширение сферы исследования и включение неопределенных факторов в число внутренних оптимизируемых па­раметров математической модели. Однако подобный подход, как

показывает опыт, не оправдывает себя из-за резкого роста трудо­емкости, а часто и нереализуемости проведения расчетов, трудно­стей сбора информации для моделирования и неизбежного загруб — ления расчетной модели при резком увеличении числа оптимизиру­емых параметров. В этом случае, по нашему мнению, конструктив­ным подходом может явиться не расширение сферы исследования, а разрыв некоторых важных внешних связей с последующей оцен­кой диапазонов их неопределенности с помощью формальных и не­формальных процедур.

Рассмотрим наиболее распространенные математические модели и методы оптимизации, используемые при исследовании воздушно­го транспорта.

Хорошо структуризованные задачи. Как. показывает опыт, хоро­шо структуризованные задачи исследования эффективности и опти­мизации систем и процессов воздушного транспорта по физическо­му содержанию принято делить на следующие типы: распредели­тельные, управления запасами, замены оборудования, массового обслуживания, выбора оптимальных режимов движения, выбора оптимальной структуры, упорядочения согласования, поиска.

Распределительные задачи являются наиболее рас­пространенными. Их содержание сводится к следующему: имеются ограниченное количество ресурсов и ряд работ, которые необходи­мо выполнить в установленные сроки с заданными показателями качества. Требуется найти такой вариант (план, стратегию) рас­пределения ресурсов по работам, при котором достигается либо максимум объема работ (максимум эффекта) при заданных затра­тах ресурсов, либо минимум затрат ресурсов при заданном объеме работ (заданном эффекте). Распределительные задачи крайне раз­нообразны по своему содержанию, и многие из них имеют специ­альные названия. Среди них—транспортная, типажа, о назначении, рюкзаке, выборе оптимального рациона, выборе оптимального при­менения ресурсов и др.

Большинство распределительных задач решаются методами линейного или’ нелинейного программирования. Одна из основных трудностей, с которой приходится встречаться при решении распре­делительных задач, — это большое число участвующих в них объ­ектов (например, много пунктов производства и пунктов потребле­ния). Для преодоления этой трудности используют блочное про­граммирование, т. е. распределяют ресурсы сначала между блока­ми (отраслями, районами),.а затем внутри блоков'(отраслей, рай­онов).

Задачи управления запасами состоят в следующем. Имеются некоторые запасы, хранение которых связано с расхода­ми. С другой стороны, отсутствие запасов приводит также к рас­ходам (иногда оно вообще недопустимо). Требуется найти такой размер запасов или порядок их пополнения, при котором расходы будут минимальны. При решении задач управления запасами рас­сматриваются следующие основные виды расходов, связанные с: хранением одного изделия (единицы запаса) в единицу времени,

отсутствием запасов, приобретением запасов, продажей излишков и т. д. Спрос на запасы может быть случайным и неслучайным, причем учет случайного характера спроса значительно усложняет задачу,

Задачи замены оборудования чрезвычайно разнооб­разны как по объему рассматриваемого оборудования, так и по со­держанию исследуемых и решаемых вопросов. Под термином обо­рудование здесь подразумевается и отдельная деталь какой-либо машины, машина в делом, комплекс машин и целое предприятие. Сущность задачи замены оборудования состоит в решении дилем­мы: продолжать ли производить и эксплуатировать старое обору­дование или же заменять его новым, более совершенным. Находя­щееся в эксплуатации оборудование с течением времени устарева­ет физически и морально и требует больших затрат на единицу производительности, чем новое. Внедрение нового оборудования требует существенных затрат на проведение исследований, разра­ботку, испытания, производство и т. д., но зато в последующем за­мена старого оборудования новым может обеспечить снижение за­трат на единицу производимой продукции и повышение эффектив­ности производства. Встает вопрос о выборе оптимальной страте­гии замены оборудования,’ т. е. о построении оптимальных про­грамм и планов технического перевооружения производства.

В практике различают физический, экономический и рациональ­ный сроки службы оборудования. Физический срок службы—эта такой срок, по достижении которого оборудование к дальнейшей эксплуатации непригодно, ремонту не подлежит и должно быть, снято с эксплуатации. Экономический срок службы — это срок, при котором обеспечиваются минимальные затраты на выполнение по­ставленных задач, включая затраты на приобретение оборудова­ния и его эксплуатацию. Рациональный срок службы оборудова­ния— это срок, учитывающий помимо экономичности также и ре­альные возможности государства по техническому перевооружению производства. Очевидно, что рациональный срок находится между экономическим и физическим сроками. Поиск оптимального срока замены оборудования заключается в определении рационального* срока с учетом ограничений производственных возможностей и фи­зического срока, при котором обеспечивается минимум себестоимо­сти производимой продукции.

Задачи массового обслуживания включают вопро­сы выбора оптимального объема, структуры и порядка работы об­служивающих систем (технического обслуживания, ремонта, пер­ронного обслуживания самолетов и т. д.) при поступлении заданий в форме потока заявок. Характерная особенность таких систем, ко­торые называются системами массового обслуживания, состоит в: том, что поток заявок и время обслуживания случайны. Поток зая­вок на обслуживание рассматривается во времени. Он может быть, стационарным, когда его характеристики во времени не меняются,, и нестационарными, когда его характеристики меняются во време­ни. Он может быть без последствий, когда число заявок в данный

момент времени не зависит от того, сколько их поступило в преды­дущий момент времени, и с последействием. Наконец, потоки могут — быть ординарные, при которых в один момент времени не может поступать несколько заявок, и неординарные, когда заявки могут поступать группами. Поток, обладающий свойствами стационарно­сти, ординарности и не имеющий последействия, называется пуас­соновским или простейшим потоком.

Анализ законов поведения системы массового обслуживания показывает, что реальной системе с произвольным потоком заявок наиболее сложно приспособиться именно к простейшему потоку за­явок. Это значит, что система, рассчитанная на простейший поток — заявок, будет надежно работать и в условиях других потоков (при одинаковой интенсивности реального и простейшего потоков зая­вок). С другой стороны, исследования показывают, что при сумми­ровании многих произвольных случайных потоков, образуется по­ток, приближающийся к простейшему.

Математические модели оптимизации систем массового обслу­живания гражданской авиации строятся, как правило, на основе простейшего потока отказов и экспоненциального закона распре­деления времени обслуживания. При формировании целевых функ­ций в качестве критериев используются: вероятность пропуска (за­держки в обслуживании) заявки; математическое ожидание числа пропущенных (задержанных) заявок за фиксированное время, чис­ла занятых каналов и длины очереди. При построении математи­ческих моделей оптимизации систем массового обслуживания рас­сматриваются однородные (состоящие из одинаковых устройств) и, неоднородные (состоящие из разных устройств), одноканальные и. многоканальные системы. Задачи массового обслуживания занима­ют важное место в организации планирования и управления нз предприятиях гражданской авиации.

Задачи выбора оптимального режима движения по своему существу сводятся к выбору маршрута (координат и скорости), удовлетворяющего заданным ограничениям по траекто­рии и техническим параметрам движущегося объекта и происхо­дящего в заданных условиях (метеорологических, гидрологических, дорожных и т. д.). При этом в качестве критерия оптимальности выступают затраты ресурсов (время, топливо, стоимость). По ха­рактеру и методам, применяемым для решения, задачи выбора — оптимальных режимов движения делятся на три следующие группы:

детерминированные задачи, где рассматривается движение ме­жду известными пунктами при строго фиксированных затратах из. пункта в пункт («задача о коммивояжере» и задача выбора опти­мального маршрута на заданной сети). Решение находят с помощью специальных методов дискретного анализа либо динамического’ программирования:

задачи выбора оптимального маршрута Движения фиксирован­ных технических устройств, не имеющие общих методов решения. Они обычно сводятся к эвристическому выбору нескольких мар-

шрутов, их оценке на моделях движения рассматриваемых объек­тов и последовательному улучшению выбранных маршрутов;

задачи выбора оптимального режима движения для вновь раз­рабатываемых технических устройств (выбора оптимальной высо­ты и скорости полета самолета, программы движения управляемых ракет и др.).

Задачи выбора массовых маршрутов тесно связаны с задачами массового обслуживания.

Задачи выбора оптимальной структуры являются важнейшими задачами процесса принятия решения’. Их основными элементами являются: построение функциональной блочной струк­туры, отражающей важнейшие элементы и связи операции и соот­ветствующей цели последней; конкретизация структуры путем раз­деления отдельных крупных элементов на более мелкие однотип­ные или неоднотипные, но решающие одинаковые задачи; упорядо­чение прохождения работ, сообщений, управляющих сигналов и усиление или ослабление функционирования отдельных элементов ■с целью минимизации времени операции при фиксированных затра­тах ресурсов. Задачи выбора структуры относятся к задачам опти­мизации на сетях.

Задачи поиска сводятся к отысканию оптимального плана поиска неисправностей, брака, полезных ископаемых, информации в библиотеке, архиве, ЭВМ и т. д. План поиска включает: объем ресурсов, выделяемых для поиска; последовательность поиска; спо­соб анализа информации, полученной при поиске. При решении данных задач минимизируются суммарные расходы, необходимые для обеспечения заданной эффективности поиска, или максимизи­руется эффективность поиска при заданных расходах.

Математические модели хорошо структуризованных задач. Ма­тематическая модель оптимального решения хорошо структуризо — ванной задачи может быть записана в следующем виде:

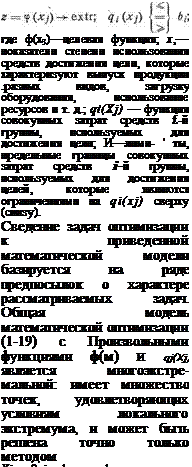(1.19)

полного перебора решений. Наиболее совершенным методом реше­ния указанной задачи является метод случайного поиска.

На основании общей модели (1.19) можно получить ряд част­ных моделей.

Модель классической задачи оптимизации:

z = f (xj) -*■ extr; qt (xj) = b-j, і = m xj >0; j = In.

В этой модели функции <p(Xj) и qi(Xj) предполагаются непре­рывными и дифференцируемыми в точке оптимума (экстремума). Однако и в этом случае возникает необходимость непосредствен­ного сравнения значений функционала в точках локального экстре­мума, т. е. необходимо производить перебор решений.

Модель сепарабельного программирования:

П

* = 2 ?,(*/>-eXtr;

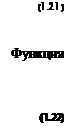І-1

п _________

2aHxi < bf, xj > 0; і — 1 m, j = In. і

Здесь целевая функция нелинейная, сепарабельная, ограничений имеет постоянные коэффициеты йц.

Модель выпуклого программирования:

z — (Xj) -> extr;

П

^aijXj « bi, Xj > 0; і = 1 m, j = In,

J-1 ..

где ф(х;)"—выпуклая функция.

Система ограничений в данной модели образует выпуклое мно­жество. Как известно, функция ф(лу) называется выпуклой, если

<f(xj+ 1 ) — 4(Xj) ><f(xj) — f(xj— 1), (1.23)

и вогнутой, если

Ч (Xj + 1) — ? (Xj) < <f (Xj) — 9 (Xj — 1). (1.24)

Выпуклая функция иногда называется выпуклой вниз, а вогну­тая—выпуклой вверх. Множество называется выпуклым, если отре­зок, соединяющий любые две точки, принадлежащие этому мно­жеству, полностью принадлежит этому множеству. В противном случае множество называется невыпуклым. Численные методы ре­шения задач выпуклого программирования базируются на идеях метода градиентного спуска.

Модель линейного программирования:

П z = 2c;A:;_vextrl /=і

(1.25)

ЩацХ) |=| bh і — т

Xj > 0, j — 1л.

 

В этой модели целевая функция ф (лу) и функция ограничений Ці(Xj) линейны. Общим универсальным методом решения задач линейного программирования является симплекс-метод. Имеется много частных методов линейного программирования. Модели и методы линейного программирования наиболее широко применя­ются в теории и практике экономико-математического моделирова­ния и оптимизации. Модель (1.25) является обобщающей моделью линейного программирования. На ее основе строятся следующие формы:

Общая

П

z = Sw->-niax v min;

(1.26)

‘У. ацх] { = } Ьі,- і = 1т; х, > 0. j — п, ;=і Ы

Стандартная

П

z— 2сЯу->-тах;

■ J=i

П

"y^aijXj « bi, і = lm; ду > 0, j = In.

i= і

Каноническая

Я.

г = 2 cJxj-*- max; .

/=і

п _

2 «у*/ = К. г = i«; •*/ > о; j — in.

7=1

Поскольку линейные функции являются частным случаем вы­пуклых функций, к задачам линейного программирования приме­нимы теоретические положения выпуклого программирования, од­нако численные методы их решения более просты и экономичны. С некоторым приближением любую функцию можно заменить ли­нейной на некотором участке и получить приближенное решение с использованием моделей линейного программирования.

Модель динамического программирования (модель Веллмана):

zk = Wu(ak, xk) +Wk+i(<fk («й, xk));
uk<=R [a]; xk Є/?[*],

где zk — целевая функция на k-м шаге управления системой; хк — состояние системы после k—1 шагов управления; ик— переменная управления, выбира­емая на fe-‘М шаге управления системой; Wh, (ик: хк) —значение критерия опти­мальности системы после k— 1 шагов управления; №),+i(<pк{ик, Хц) — условный критерий оптимальности всех последующих шагов управления системой, начи­ная с 6 +1-го шага; R[u), 7?[х] — ограничения.

Задача динамического программирования с использованием модели (1.29) формируется следующим образом. Дана некоторая система, которая с течением времени меняет свое состояние, харак­теризуемое вектором переменных состояния x(t). Переменные

.управления характеризуются вектором u(t). Задан критерии опти­мальности управления системой W (и, х). Требуется определить та — „кую программу управления системой, которая обеспечивает экстре — Мальное^значение целевой функции при ограничениях nk^R[u и xh<=R[ х].

Методы решения хорошо структуризованных задач. Для реше­ния задач оптимизации с применением рассмотренных выше мате­матических моделей в теории математического программирования разработаны следующие математические методы: дифференциаль­ного и вариационного исчислений, максимума Л. С. Понтрягина, динамического программирования (метод Веллмана), линейного, нелинейного, црлочпсленного нрограммирований, численные мето­ды поиска экстремума, эвристического программирования.

Метод дифференциального исчисления применяют при соблюдении следующих условий: целевая функция представля­ется в форме аналитической функции от переменных управления JCj, т. е.

г = <( (xj), у = In. (1.30)

ограничения на переменные управления Xj отсутствуют; решения представляют собой набор величин (но не функций времени).

Оптимальное решение находят из системы уравнений, представ­ляющих собой необходимые условия оптимальности:

d<f (xj)/dxj = 0, j~ ln. (1.31)

Решив эту систему уравнений, получают оптимальный план раз­вития (функционирования) системы

Я* = (**). (1.32)

Получив решение (1.32), необходимо провести его анализ, т. е. определить, что оно означает: максимум целевой функции, мини­мум целевой функции или ни то, ни другое. Проверку можно, заме­нить численными расчетами:

, г* =<е (х*), zi=y(xj+ Д xj), z2 = <р (x*j — bxj).

Метод вариационного исчисления применяется при наличии тех же условий, которые сформулированы для метода диф­ференциального исчисления. Его отличие от метода дифференци­ального исчисления состоит в том, что решения при данном методе получаются не в виде чисел, а в виде одной или нескольких функ­ций времени, т. е. метод вариационного исчисления представляет собой обобщение метода дифференциального исчисления на случай отыскания оптимальных функций.

Метод максимума Л. С. Понтрягина представляет собой дальнейшее развитие метода вариационного исчисления. Его применение формально не связано ни с какими ограничениями, кроме требования, чтобы целевая функция ф'(лу) и функция огра­ничений Ці (Xj) были заданы аналитически и имели конечное число разрывов. Единственное условие, вызывающее большие. затрудне-

ния в применении данного метода,— это ограничение области воз­можного изменения переменных управления Xj. Методология реше­ния задачи с применением данного принципа состоит в многократ­ном вычислении оптимальных путей и нахождения среди них тако­го, который удовлетворял бы начальным и конечным условиям.

Метод динамического программирования (ме­тод Веллмана) —это численный метод, столь же универсальный, что и принцип максимума Л. С. Понтрягина. В отличие от послед­него метод динамического. программирования легко учитывает ограничения на переменные управления Xj, не связан с аналитичес­ким описанием функций <p(xj) и qi(Xj), но требует выполнения двух условий: рассматриваемый процесс должен быть марковским, т. е. в нем предыстория не должна иметь значения для определе­ния будущих событий; целевая функция должна обладать свойст­вом аддитивности, т. е. ее величина должна быть суммой частных величин, достигаемых на отдельных этапах.

Методология решения задач с применением метода динамичес­кого программирования состоит в разбиении процесса на достаточ­но мелкие интервалы и отыскании на каждом интервале, начиная с последнего, условного оптимального управления (при всех воз­можных предложениях о результатах предыдущего шага). Когда процесс доведен до исходного состояния, то снова повторяется вся последовательность шагов от исходного состояния до конечного. При этом из множества, условно-оптимальных управлений выбира­ется одно оптимальное.

Таким обазом, метод динамического программирования заклю­чается в замене одной сложной задачи математической оптимиза­ции на множество простых.

Методы линейного программирования применя­ются, когда целевая функция ср (м)> ограничения qt (Xj) линейны и переменные управления Xj неотрицательны (Xj^O). Эти методы являются частным случаем метода динамического программирова­ния. Специфика методов линейного программирования состоит в возможности учета большого числа ограничений. Универсальным методом линейного программирования является симплекс-метод.

Методы нелинейного программирования пред­ставляют собой обобщение методов линейного программирования на случай, когда целевая функция ф(м) и ограничения q(xj) не­линейны. Общих методов решения задач нелинейного программиро­вания не существует. Наиболее полно разработан-так называемый метод, квадратичного программирования, когда целевая функция cp(xj) квадратичная, а ограничения qt(Xj) линейны.

Методы целочисленного программирования — это методы линейного программирования, когда переменные уп­равления-целые числа (например, люди, станки, машины и т. д.).

Численные методы поиска экстремума применяются в тех случаях, когда аналитические методы не разработаны или их применение затруднительно. Различают регулярные методы поис­ка, при которых поиск оптимального решения производится по

строго определенному алгоритму, и случайные методы, когда при поиске используются методы стохастического моделирования.

Регулярные методы поиска экстремума включают пассивный поиск, в^етод покоординатного подъема (спуска), градиентный ме­тод и метод наискорейшего подъема (спуска). Методы случайного поиска экстремума включают слепой последовательный и адапти­рованный случайные поиски и метод статистического моделиро­вания.

Наличие такого большого количества численных методов поис­ка экстремума (а перечислены далеко не все) объясняется тем, что — они разрабатывались применительно к конкретным задачам опти­мизации, которых достаточно много, а универсальных методов раз­работать еще не удалось.

Методы эвристического программирования со­стоят в применении неформальных методов, основанных на исполь­зовании морфологического подхода и интуиции специалистов-экс — пертов. Методы эвристического программирования, применяются для решения слабо структуризованных, а также неструктуризован — ных задач математической оптимизации, когда другие математи­ческие методы неприменимы.

Рассмотренные выше математические модели и методы оптими­зации хорошо структуризованных задач используются как матема­тическая основа методов исследования и оптимизации эффектив­ности систем и процессов воздушного транспорта.